美しい比率 貴金属比「黄金比」「白銀比」「青銅比」

 「黄金比」「白銀比」「青銅比」「白金比」「第2黄金比」とは？

限られた空間において、物体を配置する場合のバランス（比率）には一般的に美しく整って安定して感じられる比率があると言われている。これらを「貴金属比」「黄金比」「白銀比」「青銅比」などと呼び、絵画や写真の構図やデザイン、建築物の設計などに意識的に取り入れられている。また、自然界の生物の構造など（フィボナッチ数列「前の2つの数を加えると次の数になる」というルール）でもこれを見ることができる。

数学において、貴金属比（metallic ratio）とは、

1:(n＋√(n^２＋４))/2=1:X
n=1 の場合　1:(n＋√(n^２＋４))/2=(1＋√(1^２＋４))/2=1.61803399:1　第１貴金属比　黄金比

n=2 の場合　1:(n＋√(n^２＋４))/2=(2＋√(2^２＋４))/2=2.41421356:1　第２貴金属比　白銀比

n=3 の場合　1:(n＋√(n^２＋４))/2=(3＋√(3^２＋４))/2=3.30277564:1　第３貴金属比　青銅比

nを貴金属数といい、第ｎ貴金属比
すなわち、n=1 の場合　第「１」貴金属比と表される。

１～３の貴金属比を１から順に金、銀、銅とした。

第１貴金属比　黄金比（golden ratio）　  1:1.61803399

第２貴金属比　白銀比（silver ratio）　　 1:2.41421356

第３貴金属比　青銅比（bronze ratio）  　1:3.30277564

白銀比には　 第２貴金属比　白銀比とは別に、1：√2＝1：1.414を表す白銀比がある。
一般的には1：√2＝1：1.414の方を白銀比とすることの方が多い。
また二つを区別するため、第２貴金属比の白銀比（1:2.41421356）を第２白銀比と呼ぶ場合がある。これは、「第２貴金属比の方の白銀比」を短縮して「第２白銀比」になったと推測する。また白銀比（1：1.414）は「大和比」とも呼ばれ、日本の世界最古の現存する木造建築物である法隆寺の金堂や五重塔、国内の神社仏閣、仏像や仏具にも使用されており、「日本人が美しいと感じる」とされている。

貴金属比以外にも美しく整っているとされる比率はある。

白金比（platinum ratio）貴金属比ではない。正三角形の底辺の1/2の長さとその正三角形の高さの比に等しい定数 1：√3＝1：1.73205081（1：1.732）

第２黄金比 「貴金属比」ではないが、黄金比に近い比率であるため「第2黄金比」といわれている。1:(3＋√5)/2=2.61803399:1 （1：2.618）

実際にこれらの比率を利用した物、比率が見られるもの

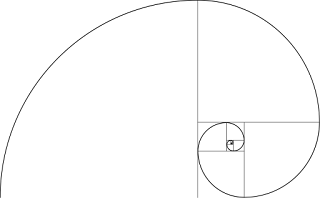
「黄金比」名刺をはじめとする様々なカード類の寸法　パルテノン神殿の高さと横幅やピラミッド高さと底辺の長さといった歴史的建造物　自然界に存在する植物の葉脈や巻貝の断面図など

「白銀比」ISO 216規格で定められる紙の寸法は 1 : √2 白銀長方形となっている　写真レンズの開口比（いわゆる絞り値、F値）の1, 1.4, 2, 2.8, 4, 5.6, 8, …